Harmonics When Plato waxed poetically about the "music of the spheres," he thought that there were mathematical relationships between the earth, the sun, the moon, and the planets which resembled the properties of a vibrating mass such as a tightened string or a tubular column of air. The ancient Greeks believed that there were astronomical ratios between earth and the heavenly bodies which were the same as the acoustic nature of a vibrating string. The source of their theory, the mathematical division of a string length, still provides one of the great timbral characteristics of stringed instruments - their ability to sound harmonics. These appropriately ethereal sounds create a wonderful contrast in color to the normal tone of a modern string instrument. However, the current notation of harmonics (flageolet in French) can be confusing to both composers and players. A discussion of the acoustic properties of harmonics and a suggestion about their notation will preface a look at some of the latest trends in their use. As an acoustic phenomenon, harmonics exist at points along the length of a stretched string. The points at which this length can be divided evenly into two, three, four, five or more segments (as according to the overtone series) are where harmonic nodes occur. If a player lightly touches a string without fully depressing it to the fingerboard at, for instance, the half-way point along its length, both segments of the string will resonate a pitch an octave higher than the open string. Likewise, by exciting either of the two nodes where a string is evenly divided into three parts, all three segments resonate including those between the finger and the peg box. In this case, a pitch sounds an octave and a fifth higher than the open string. If any one of these segments is muffled by another finger, then the harmonic sound is lost and a whining, wiry tone ensues. Even when harmonics are executed properly, they tend to be a little cranky with their tone and pitch sometimes being easy to break.
Dividing the open string into its harmonic overtones produces what are known as natural harmonics. The preceding example includes the most commonly used natural harmonics. Of course, higher overtone partials than these do exist; however, beginning with the division of the string into five segments, the intonation of the higher partials becomes noticeably and progressively more flat. Interestingly, there are certain trends now in composition that capitalize on the flat pitch of the higher harmonic overtones. It is from these flat, higher partials that alternative-tuning guru Ben Johnston derives his microtonal system. Indeed, the German composer Caspar Johannes Walter uses combinations of lower and higher partials (even as high as the 13th partial!) to focus and unfocus mists and moving clouds of intonation. Overtones also exist above any point on a string stopped by a finger. Harmonics produced by using another finger to lightly touch the string above a solidly stopped finger are called artificial or false harmonics. Normally, these are executed on the violin and viola by solidly stopping the index finger and lightly touching the node a perfect fourth higher with the little finger. This produces an actual sounding pitch two octaves higher than the stopped note. Because of their longer string lengths, the cello and the double bass typically require the thumb to stop the string and the ring finger to excite the harmonic. In fact, the string length on the double bass is so long that the interval of the perfect fourth can only begin to be reached up in the higher positions on the fingerboard. The history of notating harmonics is rather interesting. Such great, early 20th-Century orchestrators as Stravinsky, Debussy, Ravel, and Scoenberg all had certain proclivities for the special sound of string harmonics. Typically, they would use the symbol '°' directly above or below the notehead of the pitch they actually desired to have sounded as a harmonic. This practice is rather old-fashioned and in quite a few instances can be confusing. There are examples in some orchestral string parts where Stravinsky and Ravel actually wrote harmonics on pitches that cannot be rendered in the octave indicated. String players themselves are often unschooled about harmonics and many times do not know how to produce a given pitch in the proper octave. Occasionally, an entire string section in an orchestra will have to be told how to execute a written harmonic. There remain quite a few different strategies in notating harmonics. Perhaps the clearest is the way in which Elliott Carter writes them. He always includes three notations no matter whether writing natural harmonics or artificial. First, in the proper rhythm, he writes the pitch of the open or the stopped string. Second, he indicates in tablature the spot on the fingerboard where the node is to be lightly touched. Tablature notation uses an unfilled-in diamond shape which tells the player where to place the finger. For a duration shorter than a whole note, the tablature is connected to the stopped pitch by a stem. Finally, he always includes the actual sounding pitch of the harmonic in its correct octave. This is indicated in parenthesis on the staff above the tablature or on an additional staff. This manner of notating harmonics leaves no doubt as to what pitch and in which octave it is to be sounded. In repetitive passages, the sounding pitch need not be laboriously duplicated.
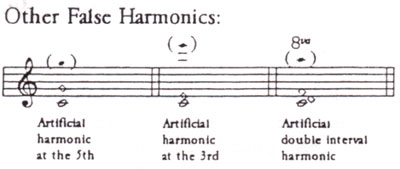
Contemporary techniques include an incredible number of unique applications of harmonics. These begin with artificial harmonics excited at intervals other than a fourth. Different artificial harmonics can be produced by touching a perfect fifth above the stopped pitch which sounds an octave higher than the note under the touched node. Another artificial harmonic can be produced by touching a major third above the stopped pitch which then sounds two octaves above the lightly touched note. On the double bass, the major third harmonic is used quite often because its smaller size is more easily negotiable on that instrument's enormously long string length. 200 years ago in his innovative cello treatise, Louis Duport, for whom Beethoven wrote a couple of early sonatas, suggested a radical artificial harmonic where two nodes, one a major second and the other a perfect fourth, are lightly touched simultaneously above the stopped pitch supposedly sounding a pitch two octaves and a major sixth above the stopped note. Such double-node harmonics are all but impossible to perform consistently and usually produce some sort of "found sound" as opposed to any predictable pitch which can be more easily produced by another artificial harmonic.
Slides between pitches or glissandos work enormously well with artificial harmonics. The quintessential example of sliding harmonics comes from Iannis Xenakis's Nomos Alpha for solo cello. Their sometimes rapid pace in the piece makes the sounds seem like they are being hurtled into space by an atomic particle generator. With a slower pace but with a similar impact, Dorothy Hindman uses artificial harmonic glissandos in drowningXnumbers for amplified cello. Notice how she also uses note stems to help indicate the rhythmic duration of the slide.
Perhaps the most famous harmonic glissandos are the "sea-gull" effects in the cello part of George Crumb's trio for flute, cello, and piano, Vox Balaenae. In this instance, the exact distance between the fingers is maintained during the downward slide so that different overtone partials are phased out of and into different harmonic nodes. This effect occurs because the actual distance descending between pitches on the instrument increases logarithmically against the unchanging spacing in the hand. Monroe Golden at the beginning of his Fantasy for solo cello writes a unique set of harmonic glissandos where the stopped finger and the lightly touched finger slide independently of each other producing an effect like moving from one AM radio station to another.
Another famous artificial harmonic glissando is the "seagull effect" from Vox Balaenae by George Crumb.
When writing harmonics, there are some considerations which are important to keep in mind. First of all, every different artificial harmonic must be executed with a different setting of the left hand. This makes the technique less facile for both rapid passages and extremely disjunct intervals. False harmonics are by far and away more difficult to play than natural harmonics. Further, artificial harmonics become progressively more difficult to excite in the high register especially in the fourth octave and beyond because of the very short string length. Pizzicato and plucking work well on natural harmonics but produce only dull thuds on false harmonics. Similarly, double stops (sounding two different pitches simultaneously) also work well on natural harmonics but are totally problematic on artificial harmonics. Double stops that include mixed combinations of open strings, stopped notes, natural, or false harmonics can be played but should be conceived with the greatest possible attention to the ease of execution. Warning - the combinations must be kept simple allowing time for the left hand to configure the double stop and using low harmonic partials because there is a incredibly great potential for writing something totally impossible to render. In spite of such caution, various harmonic techniques do extend the range and timbral palette of string instruments helping them remain potent sound boxes for the next millennium. The flute-like quality of harmonics provides a fantastic contrast in color to the normal string tone. The purity of the way they sound suggests many metaphors that can inspire the musical architecture of a composition. The proper use of harmonics is a sign of sophistication to a player and a wonderful delight to the ears of an audience.
|